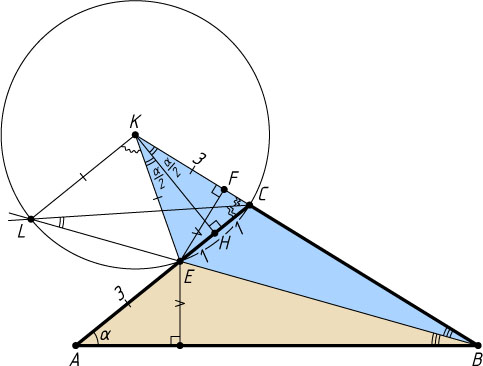
666. В треугольнике ABC
угол C
— тупой; биссектриса BE
угла B
делит сторону AC
на отрезки AE=3
, EC=2
. Известно, что точка K
, лежащая на продолжении стороны BC
за вершину C
, является центром окружности, проходящей через точки C
, E
и точку пересечения биссектрисы угла B
с биссектрисой угла ACK
. Найдите расстояние от точки E
до стороны AB
.
Ответ. \frac{4\sqrt{2}}{3}
.
Указание. Докажите равенство треугольников BKE
и BAE
.
Решение. Пусть биссектриса угла ABC
пересекается с биссектрисой угла ACK
в точке L
. Обозначим \angle BKE=\alpha
.
Поскольку CKE
— центральный угол окружности, о которой говорится в условии задачи, а угол CLE
— вписанный, то
\angle CLE=\frac{1}{2}\angle CKE=\frac{\alpha}{2}.
Из равнобедренного треугольника CKE
находим, что
\angle KCE=90^{\circ}-\frac{\alpha}{2}.
Тогда
\angle LCE=\frac{1}{2}\angle KCE=\frac{1}{2}\left(90^{\circ}-\frac{\alpha}{2}\right)=45^{\circ}-\frac{\alpha}{4},
\angle ACB=180^{\circ}-\angle KCE=180^{\circ}-\left(90^{\circ}-\frac{\alpha}{2}\right)=90^{\circ}+\frac{\alpha}{2},
\angle EKL=2\angle LCE=90^{\circ}-\frac{\alpha}{2},
\angle BCL=\angle ACB+\angle LCE=90^{\circ}+\frac{\alpha}{2}+45^{\circ}-\frac{\alpha}{4}=135^{\circ}+\frac{\alpha}{4},
\angle CBL=180^{\circ}-\angle BLC-\angle BCL=180^{\circ}-\frac{\alpha}{2}-\left(135^{\circ}+\frac{\alpha}{4}\right)=45^{\circ}-\frac{3}{4}\alpha,
\angle ABC=2\angle CBL=90^{\circ}-\frac{3}{2}\alpha,
\angle BAC=180^{\circ}-\angle ABC-\angle ACB=180^{\circ}-\left(90^{\circ}-\frac{3}{2}\alpha\right)-\left(90^{\circ}+\frac{\alpha}{2}\right)=\alpha.
Значит, треугольник BKE
равен треугольнику BAE
. Поэтому KC=KE=AE=3
.
Поскольку точка E
лежит на биссектрисе угла ABK
, то она равноудалена от сторон угла, поэтому искомое расстояние равно высоте EF
равнобедренного треугольника KCE
со сторонами KC=KE=3
и CE=2
.
Пусть KH
— также высота этого треугольника. Тогда
KH=\sqrt{9-1}=2\sqrt{2},
а так как CK\cdot EF=CE\cdot KH
, то
EF=\frac{CE\cdot KH}{CK}=\frac{2\cdot2\sqrt{2}}{3}=\frac{4\sqrt{2}}{3}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1972, вариант 3, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 259
