667. В прямоугольном секторе AOB
проведена хорда AB
и в образовавшийся сегмент вписан квадрат. Найдите отношение стороны квадрата к радиусу окружности, которая касается хорды AB
, дуги AB
и стороны квадрата, перпендикулярной хорде AB
.
Ответ. \frac{5}{12}\sqrt{110+60\sqrt{2}}=\frac{(\sqrt{5}+\sqrt{2})(3+\sqrt{5})}{6\sqrt{2}}
.
Указание. Выразите радиус сектора через сторону квадрата. Для этого рассмотрите прямоугольный треугольник с вершинами в точке O
, середине стороны квадрата, параллельной хорде AB
, и в вершине квадрата, лежащей на дуге.
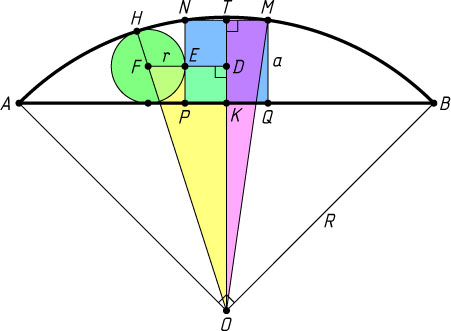
Решение. Пусть a
— сторона квадрата MNPQ
(P
и Q
принадлежат хорде AB
), R
— радиус сектора, F
— центр указанной окружности, r
— её радиус, E
и H
— точки касания этой окружности со стороной NP
квадрата и дугой AB
, T
— середина MN
, K
— середина хорды AB
, D
— точка пересечения прямой FE
с отрезком OT
.
В прямоугольном треугольнике OMT
известно, что
OM^{2}=OT^{2}+MT^{2},~\mbox{или}~R^{2}=(OK+KT)^{2}+\frac{1}{2}MN^{2},
R^{2}=\left(\frac{R}{\sqrt{2}}+a\right)^{2}+\frac{a^{2}}{4},~2R^{2}-4aR\sqrt{2}-5a^{2}=0.
Из этого уравнения находим, что R=\frac{5a\sqrt{2}}{2}
. В прямоугольном треугольнике ODF
известно, что
OF=OH-FH=R-r,~FD=FE+ED=r+\frac{a}{2},
OD=OK+KD=\frac{R}{\sqrt{2}}+r.
По теореме Пифагора
OF^{2}=OD^{2}+DF^{2},~\mbox{или}~(R-r)^{2}=\left(\frac{R}{\sqrt{2}}+r\right)^{2}+\left(r+\frac{a}{2}\right)^{2}.
Подставим в это уравнение R=\frac{5a\sqrt{2}}{2}
. После упрощения получим уравнение
6a^{2}-ar(5\sqrt{2}+6)-r^{2}=0,
из которого находим \frac{a}{r}
.
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) МГУ. — 1972, вариант 2, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 219
