668. В прямоугольном секторе AOB
из точки B
как из центра проведена дуга OC
(C
— точка пересечения этой дуги с дугой AB
) радиуса BO
. Окружность S_{1}
касается дуги AB
, дуги OC
и прямой OA
, а окружность S_{2}
касается дуги AB
, прямой OA
и окружности S_{1}
. Найдите отношение радиуса окружности S_{1}
к радиусу окружности S_{2}
.
Ответ. \frac{4(2\pm\sqrt{3})}{3}
.
Указание. Отрезок общей внешней касательной к двум касающимся окружностям радиусов r
и R
, заключённый между точками касания, равен 2\sqrt{rR}
.
Решение. Пусть R
— радиус сектора, P
— центр окружности S_{1}
, r
— её радиус, M
и D
— её точки касания с дугой AB
и прямой OA
соответственно, x
— радиус окружности S_{2}
, Q
— её центр, K
и N
— её точки касания с дугой AB
и прямой OA
соответственно.
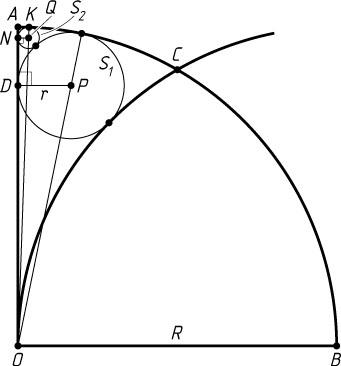
Рассмотрим случай, когда точка N
лежит на продолжении отрезка OD
за точку D
(рис. 1).
В прямоугольном треугольнике ODP
известно (см. задачу 365), что
OD=2\sqrt{rR},~OP=OM-MP=R-r,~DP=r.
По теореме Пифагора
OP^{2}=OD^{2}+DP^{2},~\mbox{или}~(R-r)^{2}=(2\sqrt{rR})^{2}+r^{2}.
Отсюда находим, что R=6r
.
В прямоугольном треугольнике OQN
известно, что
OQ=OK-KQ=R-x=6r-x,~QN=x,
ON=OD+DN=2\sqrt{rR}+2\sqrt{rx}.
По теореме Пифагора
OQ^{2}=QN^{2}+ON^{2},~\mbox{или}~(6r-x)^{2}=x^{2}+4(r\sqrt{6}+\sqrt{rx})^{2},
или
3\left(\frac{r}{x}\right)-2\sqrt{6}\sqrt{\frac{r}{x}}-4=0.
Отсюда находим, что
\sqrt{\frac{r}{x}}=\frac{\sqrt{6}+3\sqrt{2}}{3}=\frac{\sqrt{2}+\sqrt{6}}{\sqrt{3}}.
Следовательно,
\frac{r}{x}=\frac{4(2+\sqrt{3})}{3}.
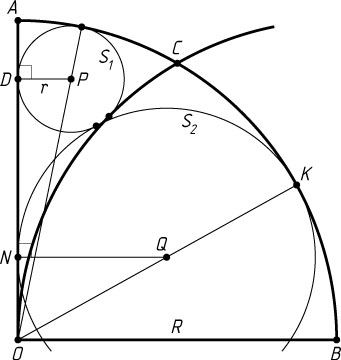
Пусть теперь точка N
лежит между точками O
и D
(рис. 2). Тогда ON=OD-DN=2\sqrt{rR}-2\sqrt{rx}
. Это приводит к уравнению
3\left(\frac{r}{x}\right)+2\sqrt{6}\sqrt{\frac{r}{x}}-4=0,
из которого находим, что
\frac{r}{x}=\frac{4(2-\sqrt{3})}{3}.
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) МГУ. — 1972, вариант 1, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 219
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.46, с. 71

