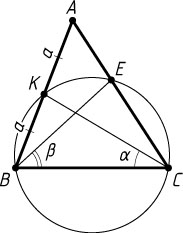
678. Через вершины B
и C
треугольника ABC
проведена окружность, которая пересекает сторону AB
в точке K
и сторону AC
в точке E
. Найдите AE
, зная, что AK=KB=a
, \angle BCK=\alpha
, \angle CBE=\beta
.
Ответ. \frac{a}{2\sin\alpha}\left(\sqrt{\sin^{2}\beta+8\sin^{2}\alpha}-\sin\beta\right)
.
Указание. Произведение всей секущей на её внешнюю часть для данной точки и данной окружности постоянно.
Решение. Обозначим через R
радиус данной окружности. Поскольку треугольник BCK
вписан в окружность, то
R=\frac{a}{2\sin\alpha}.
Поскольку треугольник BCE
также вписан в эту окружность, то
CE=2R\sin\beta=\frac{a\sin\beta}{\sin\alpha}.
Поскольку AC\cdot AE=AB\cdot AK
, то
\left(AE+\frac{a\sin\beta}{\sin\alpha}\right)AE=2a^{2},
или
AE^{2}+\frac{a\sin\beta\cdot AE}{\sin\alpha}-2a^{2}=0.
Откуда находим, что
AE=\frac{a}{2\sin\alpha}\left(\sqrt{\sin^{2}\beta+8\sin^{2}\alpha}-\sin\beta\right)
Источник: Вступительный экзамен на географический факультет МГУ. — 1972, вариант 3, № 5
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 49
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.12, с. 94
