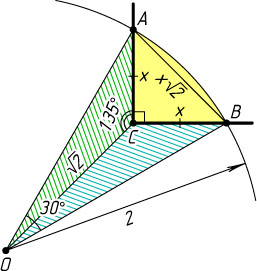
681. Вне прямого угла с вершиной C
, на продолжении его биссектрисы взята точка O
, причём OC=\sqrt{2}
. С центром в точке O
построена окружность радиуса 2. Найдите площадь фигуры, ограниченной сторонами угла и дугой окружности, заключённой между ними.
Ответ. \frac{\pi}{3}-\sqrt{2}+1
.
Указание. Найдите косинус угла AOB
Решение. Пусть A
и B
— точки пересечения окружности со сторонами угла. Обозначим AC=BC=x
.
По теореме косинусов
AO^{2}=AC^{2}+OC^{2}-2AC\cdot OC\cos135^{\circ},
или
4=x^{2}+2+2x\sqrt{2}\cdot\frac{\sqrt{2}}{2},~x^{2}+2x-2=0.
Из этого уравнения находим, что x=\sqrt{3}-1
. Тогда
AB=x\sqrt{2}=\sqrt{2}(\sqrt{3}-1).
По теореме косинусов из треугольника AOB
находим, что
\cos\angle AOB=\frac{OA^{2}+OB^{2}-AB^{2}}{2OA\cdot OB}=\frac{4+4-2(\sqrt{3}-1)^{2}}{8}=\frac{\sqrt{3}}{2}.
Поэтому \angle AOB=30^{\circ}
и площадь сектора AOB
равна \frac{4\pi}{12}=\frac{\pi}{3}
.
Искомая площадь равна разности между площадью этого сектора и суммой площадей треугольников ACO
и BCO
, т. е.
\frac{\pi}{3}-2\cdot\frac{1}{2}CA\cdot CO\sin135^{\circ}=\frac{\pi}{3}-\sqrt{3}+1.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1972, № 4, вариант 1
