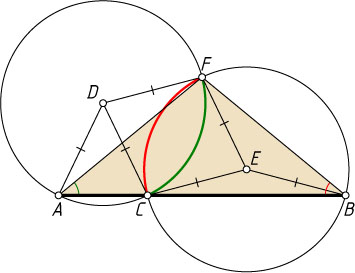
687. Внутри отрезка AB
взята точка C
. По одну сторону от прямой AB
построены равнобедренные треугольники ADC
и CEB
, причём AD=DC=CE=EB
. Точка F
находится на расстоянии, равном AD
, от вершин D
и E
и не совпадает с точкой C
. Докажите, что AF=FB
.
Указание. Проведите две окружности с центрами D
и E
и радиусами, равными AD
.
Решение. Проведём две окружности с центрами D
и E
и радиусами, равными AD
. Тогда \angle FAB=\angle FBA
как вписанные углы, опирающиеся на равные дуги равных окружностей. Следовательно, треугольник AFB
— равнобедренный и FA=FB
.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1972, № 4, вариант 4
