690. В прямоугольный треугольник ABC
вписан квадрат так, что две его вершины лежат на гипотенузе AB
, а две другие — на катетах. Радиус круга, описанного около треугольника ABC
, относится к стороне квадрата как 13:6
. Найдите углы треугольника.
Ответ. \arctg3
, \arctg\frac{1}{3}
.
Указание. Выразите гипотенузу треугольника через сторону квадрата и тангенс острого угла треугольника.
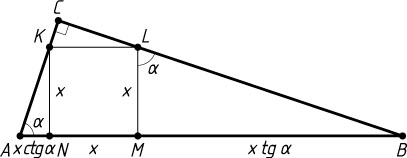
Решение. Пусть вершины M
и N
квадрата MNKL
лежат на гипотенузе AB
(M
— между N
и B
). Обозначим сторону квадрата через x
, \angle A=\alpha
, радиус описанной окружности треугольника ABC
— через R
.
Из прямоугольных треугольников ANK
и BML
находим, что
AN=\frac{x}{\tg\alpha},~BM=x\tg\alpha.
Поэтому
2R=AB=AN+NM+MB=\frac{x}{\tg\alpha}+x+x\tg\alpha.
Тогда
\frac{1}{\tg\alpha}+\tg\alpha+1=\frac{2R}{x}=\frac{13}{3},
или
3\tg^{2}\alpha-10\tg\alpha+3=0.
Из этого уравнения находим, что \tg\alpha=3
или \tg\alpha=\frac{1}{3}
.
Источник: Вступительный экзамен на химический факультет МГУ. — 1973, вариант 2, № 5
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 167
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 13.46, с. 131
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 13.46.1, с. 142
