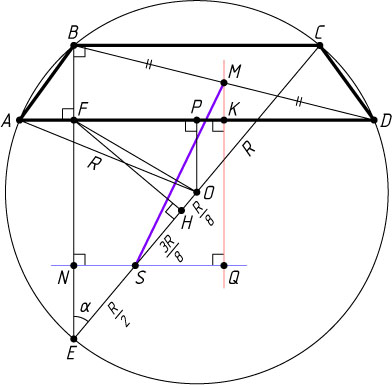
693. В окружность с центром O
вписана трапеция ABCD
(BC\parallel AD
). В этой же окружности проведены диаметр CE
и хорда BE
, пересекающая AD
в точке F
. Точка H
— основание перпендикуляра, опущенного из точки F
на CE
, S
— середина отрезка EO
, M
— середина BD
. Известно, что радиус окружности равен R
, а CH=\frac{9}{8}R
. Найдите SM
.
Ответ. \frac{3R}{2\sqrt{2}}
.
Указание. Через точку H
проведите прямую, параллельную BE
, а через точку S
— прямую, параллельную AD
. Пусть Q
— точка пересечения проведённых прямых. Обозначьте \angle BEC=\alpha
. Выразите через \alpha
отрезки SQ
и MQ
.
Решение. Поскольку \angle CBE=90^{\circ}
, то BE\perp AD
. Через точку M
проведём прямую, параллельную BE
, а через точку S
— прямую, параллельную AD
. Пусть Q
— точка пересечения проведённых прямых. Отрезок SM
будем искать из прямоугольного треугольника MQS
.
Обозначим \angle BEC=\alpha
. Тогда
FH=EH\tg\alpha=(EC-CH)\tg\alpha=\frac{7}{8}R\tg\alpha,
FO^{2}=FH^{2}+HO^{2}=\left(\frac{R^{2}}{64}\right)(49\tg^{2}\alpha+1).
Пусть P
— проекция центра O
на хорду AD
. Тогда
FP=\frac{1}{2}BC=\frac{1}{2}\cdot2R\sin\alpha=R\sin\alpha,
OP^{2}=OF^{2}-FP^{2}=\left(\frac{R^{2}}{64}\right)(49\tg^{2}\alpha+1)-R^{2}\sin\alpha,
AP^{2}=AO^{2}-OP^{2}=R^{2}-\left(\frac{R^{2}}{64}\right)(49\tg^{2}\alpha+1)+R^{2}\sin\alpha.
Пусть N
— точка пересечения прямых BE
и QS
, K
— точка пересечения прямых MQ
и AD
. Тогда
NQ=FK=\frac{1}{2}FD=\frac{1}{4}(AD+BC)=\frac{1}{2}\left(\frac{1}{2}AD+\frac{1}{2}BC\right)=\frac{1}{2}\left(AP+\frac{1}{2}BC\right)=
=\frac{1}{2}\left(R\sqrt{1-\frac{49\tg^{2}\alpha+1}{64}+\sin^{2}\alpha}+R\sin\alpha\right).
Следовательно,
QS=QN-NS=QN-SE\sin\alpha=QN-\frac{1}{2}R\sin\alpha=\frac{1}{2}R\sqrt{1-\frac{49\tg^{2}\alpha+1}{64}+\sin^{2}\alpha},
MQ=MK+KQ=\frac{1}{2}BF+FN=\frac{1}{2}(BE-EF)+(FE-NE)=
=\frac{1}{2}BE+\frac{1}{2}FE-NE=R\cos\alpha+\frac{EH}{2\cos\alpha}-EO\cos\alpha=
=R\cos\alpha+\frac{1}{2}\cdot\frac{7}{8}\cdot\frac{R}{\cos\alpha}-\frac{1}{2}R\cos\alpha=\frac{1}{2}R\left(\cos\alpha+\frac{7}{8\cos\alpha}\right).
Поэтому
SM^{2}=MQ^{2}+SQ^{2}=
=\frac{R^{2}}{4}\left(1-\frac{49\tg^{2}\alpha+1}{64}+\sin^{2}\alpha+\left(\cos\alpha+\frac{7}{8\cos\alpha}\right)^{2}\right)=\frac{9R^{2}}{8}.
