696. Две окружности с центрами O_{1}
, O_{2}
и радиусами 32, пересекаясь, делят отрезок O_{1}O_{2}
на три равные части. Найдите радиус окружности, которая касается изнутри обеих окружностей и касается отрезка O_{1}O_{2}
.
Ответ. 7.
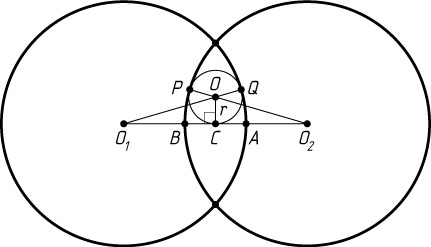
Решение. Обозначим через r
радиус искомой окружности. Пусть O
— её центр, Q
и P
— точки касания соответственно с первой и второй окружностями, C
— точка касания с прямой O_{1}O_{2}
, A
и B
— точки пересечения соответственно первой и второй окружностей с отрезком O_{1}O_{2}
. Тогда
O_{1}A=AB=BO_{2}=16,~O_{1}C=24,
OC=r,~O_{1}O=O_{1}Q-OQ=32-r.
По теореме Пифагора из прямоугольного треугольника O_{1}CO
находим, что
O_{1}O^{2}=O_{1}C^{2}+OC^{2},~\mbox{или}~(32-r)^{2}=24^{2}+r^{2}.
Из этого уравнения находим, что r=7
.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1973, вариант 2, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 77
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.21, с. 69
