698. Окружность радиуса 1+\sqrt{2}
описана около равнобедренного прямоугольного треугольника. Найдите радиус окружности, которая касается катетов этого треугольника и внутренним образом касается окружности, описанной около него.
Ответ. 2.
Указание. Пусть M
и N
— точки касания искомой окружности с катетами AC
и BC
треугольника ABC
, Q
— центр этой окружности. Тогда четырёхугольник QMCN
— квадрат.
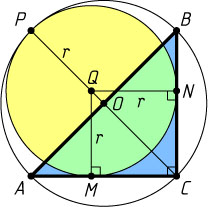
Решение. Пусть r
— радиус искомой окружности, Q
— её центр, M
, N
— точки касания с катетами соответственно AC
и BC
треугольника ABC
, O
— центр описанной окружности, P
— точка касания окружностей. Тогда точки O
и Q
лежат на диаметре CP
, а четырёхугольник QMCN
— квадрат со стороной r
. Поэтому
CQ=r\sqrt{2},~CQ+QP=CP,~r\sqrt{2}+r=2(1+\sqrt{2}).
Отсюда находим, что
r=\frac{2(1+\sqrt{2})}{\sqrt{2}+1}=2.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1973, вариант 4, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 78
