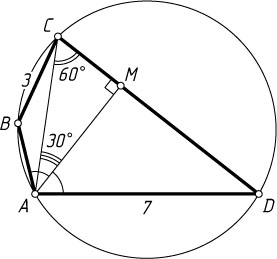
701. В выпуклом четырёхугольнике ABCD
проведена диагональ AC
, AD=7
, BC=3
, \angle ACD=60^{\circ}
. Известно, что точки A
, B
, C
, D
лежат на одной окружности, и перпендикуляр, проведённый из точки A
к стороне CD
, делит угол BAD
пополам. Найдите диагональ AC
.
Ответ. 5.
Указание. Найдите синус угла ADC
.
Решение. Пусть AM
— перпендикуляр, опущенный из точки A
на сторону CD
. Луч AC
проходит между сторонами угла BAM
, поэтому
\angle BAM=\angle BAC+\angle CAM.
Пусть R
— радиус описанной окружности четырёхугольника ABCD
. Тогда
R=\frac{AD}{2\sin\angle ACD}=\frac{7}{\sqrt{3}},
\sin\angle BAC=\frac{BC}{2R}=\frac{3\sqrt{3}}{14},~\angle CAM=30^{\circ}.
Поэтому
\sin\angle MAD=\sin(\angle BAC+30^{\circ})=\frac{3\sqrt{3}}{14}\cdot\frac{\sqrt{3}}{2}+\frac{1}{2}\cdot\frac{13}{14}=\frac{11}{14},
\sin\angle ADC=\cos\angle MAD=\frac{5\sqrt{3}}{14}.
Следовательно,
AC=2R\sin\angle ADC=\frac{2\cdot7}{\sqrt{3}}\cdot\frac{5\sqrt{3}}{14}=5.
