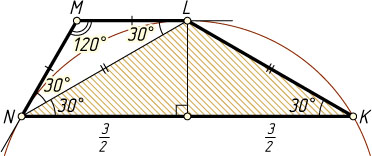
702. Стороны KN
и LM
трапеции KLMN
параллельны, причём KN=3
, а угол M
равен 120^{\circ}
. Прямые LM
и MN
являются касательными к окружности, описанной около треугольника KLN
. Найдите площадь треугольника KLN
.
Ответ. \frac{3\sqrt{3}}{4}
.
Указание. Докажите, что треугольник KLN
— равнобедренный.
Решение. Отрезки ML
и MN
равны как касательные, проведённые из одной точки к окружности. Поэтому
\angle MNL=\angle MLN=30^{\circ},~\angle LNK=\angle MLN=30^{\circ}.
Поскольку угол LKN
— вписанный, а угол MNL
— угол между касательной и хордой LN
, то \angle LKN=30^{\circ}
. Следовательно, треугольник KLN
— равнобедренный. Его высота равна
\frac{1}{2}KN\cdot\tg30^{\circ}=\frac{3}{2}\cdot\frac{\sqrt{3}}{3}=\frac{\sqrt{3}}{2}.
Следовательно,
S_{\triangle KLN}=\frac{1}{2}\cdot3\cdot\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{4}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1989, вариант 2, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 18
