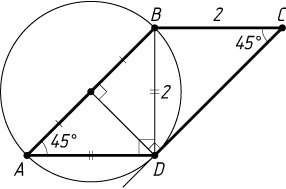
703. В параллелограмме ABCD
диагональ BD
равна 2, угол C
равен 45^{\circ}
, причём прямая CD
касается окружности, описанной около треугольника ABD
. Найдите площадь параллелограмма ABCD
.
Ответ. 4.
Указание. Докажите, что BD\perp BC
.
Решение. Ясно, что \angle A=\angle C=45^{\circ}
. Угол BAD
вписан в окружность, а \angle BDC
— угол между касательной и хордой BD
, поэтому
\angle BDC=\angle A=45^{\circ}.
Следовательно, \angle CBD=90^{\circ}
. Значит,
S_{ABCD}=BC\cdot BD=2\cdot2=4.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1989, вариант 1, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 20
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 13.42, с. 130
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 13.42.1, с. 141
