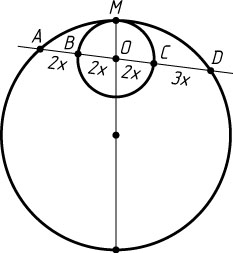
705. Две окружности касаются внутренним образом. Прямая, проходящая через центр меньшей окружности, пересекает большую окружность в точках A
и D
, а меньшую — в точках B
и C
. Найдите отношение радиусов окружностей, если AB:BC:CD=2:4:3
.
Ответ. 3.
Указание. Примените теорему о произведениях отрезков пересекающихся хорд.
Решение. Пусть M
— точка касания окружностей, r
и R
(r\lt R
) — их радиусы, O
— центр меньшей из них. Обозначим: AB=2x
, BC=4x
, CD=3x
. Тогда
r=OB=OC=2x,~DO\cdot OA=MO(2R-MO),~\mbox{или}~5x\cdot4x=2x(2R-2x).
Следовательно,
5x=R-x,~R=6x,~\frac{R}{r}=\frac{6x}{2x}=3.
Источник: Вступительный экзамен в МФТИ. — 1976, билет 1, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 76-1-3, с. 184
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.27, с. 69
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 18, с. 140
