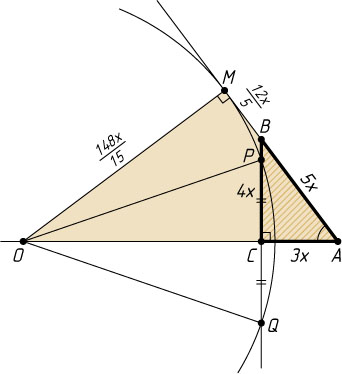
707. В прямоугольном треугольнике ABC
угол C
— прямой, AC:AB=3:5
. Окружность с центром на продолжении катета AC
за точку C
касается продолжения гипотенузы AB
за точку B
и пересекает катет BC
в точке P
, причём BP:PC=1:4
. Найдите отношение радиуса окружности к катету BC
.
Ответ. \frac{37}{15}
.
Указание. Примените теорему о касательной и секущей.
Решение. Положим AC=3x
, AB=5x
. Тогда
BC=4x,~\tg\angle A=\frac{4}{3},~BP=\frac{4x}{5},~PC=\frac{16x}{5}.
Пусть Q
— вторая точка пересечения прямой BC
с указанной окружностью, O
— центр этой окружности, M
— точка касания с продолжением гипотенузы AB
. Тогда
BM=\sqrt{BP\cdot BQ}=\sqrt{\frac{144x^{2}}{25}}=\frac{12x}{5},
OM=AM\tg\angle A=\left(5x+\frac{12x}{5}\right)\cdot\frac{4}{3}=\frac{37\cdot4x}{15}.
Следовательно, \frac{OM}{BC}=\frac{37}{15}
.
Источник: Вступительный экзамен в МФТИ. — 1976, билет 4, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 76-4-3, с. 185
