709. В равнобедренную трапецию, основания которой равны a
и b
(a\gt b
), можно вписать окружность. Найдите расстояние между центрами вписанной и описанной около этой трапеции окружностей.
Ответ. \frac{a^{2}-b^{2}}{8\sqrt{ab}}
.
Указание. Опустите перпендикуляры из центров указанных окружностей на одну из боковых сторон трапеции, соедините центр вписанной окружности с серединой этой боковой стороны и рассмотрите полученные подобные треугольники.
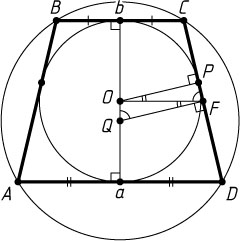
Решение. Пусть O
и Q
— центры вписанной и описанной окружностей трапеции ABCD
с основаниями AD=a
и BC=b
, P
— точка касания вписанной окружности с боковой стороной CD
, F
— середина CD
.
Прямая OQ
— серединный перпендикуляр отрезков BC
и AD
. Треугольники OPF
и FOQ
подобны по двум углам. Поэтому
\frac{OQ}{OF}=\frac{PF}{OP},~OF=\frac{1}{2}\cdot\frac{1}{2}(a+b)=\frac{a+b}{4},
PF=CF-CP=\frac{a+b}{4}-\frac{b}{2}=\frac{a-b}{4},
OP=r=\sqrt{CP\cdot PD}=\frac{\sqrt{ab}}{2}
(см. задачу 656). Следовательно,
OQ=OF\cdot\frac{PF}{OP}=\frac{(a+b)(a-b)}{8\sqrt{ab}}=\frac{a^{2}-b^{2}}{8\sqrt{ab}}.
Источник: Вступительный экзамен на физико-химический факультет МИСиС. — 1979, № 4
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 4.46.1, с. 40
