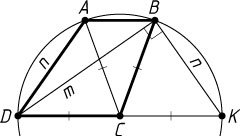
712. Диагональ BD
трапеции ABCD
равна m
, а боковая сторона AD
равна n
. Найдите основание CD
, если известно, что основание, диагональ и боковая сторона трапеции, выходящие из вершины C
, равны между собой.
Ответ. \frac{1}{2}\sqrt{m^{2}+n^{2}}
.
Указание. Точки D
, A
и B
лежат на окружности с центром в точке C
.
Решение. Поскольку CD=CA=CB
, то точки D
, A
и B
лежат на окружности с центром в точке C
и радиусом, равным CD
.
Пусть K
— вторая точка пересечения прямой CD
с этой окружностью. Тогда DK
— диаметр, AB\parallel DK
. Поэтому BK=AD=n
, а \angle DBK=90^{\circ}
. По теореме Пифагора
DK=\sqrt{DB^{2}+BK^{2}}=\sqrt{m^{2}+n^{2}}.
Следовательно,
CD=\frac{1}{2}DK=\frac{1}{2}\sqrt{m^{2}+n^{2}}.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1977, вариант 4, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1983. — с. 74
Источник: Говоров В. М. и др. Сборник конкурсных задач по математике. — М.: Наука, 1986. — № 31, с. 186
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.35, с. 32
