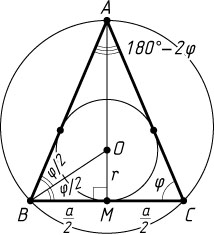
713. Угол при основании равнобедренного треугольника равен \varphi
. Найдите отношение радиуса вписанной в данный треугольник окружности к радиусу описанной окружности.
Ответ. \tg\frac{\varphi}{2}\sin2\varphi=2(1-\cos\varphi)\cos\varphi
.
Указание. Выразите радиусы окружностей через основание треугольника.
Решение. Обозначим основание BC
равнобедренного треугольника ABC
через a
, радиусы вписанной и описанной окружностей — r
и R
соответственно, центр вписанной окружности — O
, середину BC
— M
. Тогда
R=\frac{BC}{2\sin\angle BAC}=\frac{a}{2\sin(180^{\circ}-2\varphi)}=\frac{a}{2\sin2\varphi},
r=OM=BM\tg\frac{1}{2}\angle B=\frac{a}{2}\tg\frac{\varphi}{2}.
Следовательно,
\frac{r}{R}=\tg\frac{\varphi}{2}\sin2\varphi=\frac{\sin\frac{\varphi}{2}}{\cos\frac{\varphi}{2}}\cdot2\sin\varphi\cos\varphi=
=\frac{\sin\frac{\varphi}{2}}{\cos\frac{\varphi}{2}}\cdot4\sin\frac{\varphi}{2}\cos\frac{\varphi}{2}\cos\varphi=4\sin^{2}\frac{\varphi}{2}\cos\varphi=2(1-\cos\varphi)\cos\varphi.
Источник: Вступительный экзамен на географический факультет МГУ. — 1966, вариант 3, № 3
Источник: Моденов П. С. Экзаменационные задачи по математике с анализом их решения. — М.: Просвещение, 1969. — вариант 3, № 3, с. 49
Источник: Вступительный экзамен в МИНХ. — 1979
Источник: Говоров В. М. и др. Сборник конкурсных задач по математике. — М.: Наука, 1986. — № 37, с. 187
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.22, с. 87
