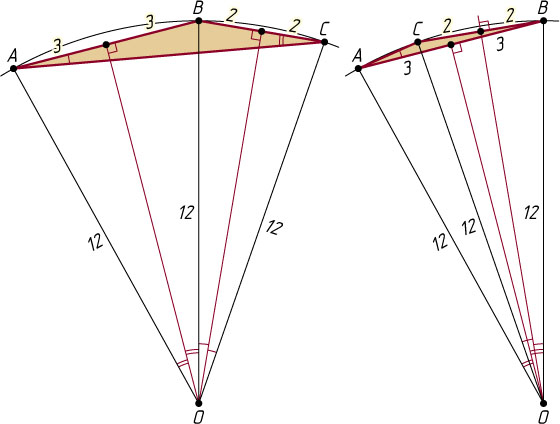
715. В круге радиуса 12 хорда AB=6
, а хорда BC=4
. Найдите хорду, соединяющую концы дуги AC
.
Ответ. \sqrt{35}\pm\sqrt{15}
.
Указание. Примените формулу a=2R\sin\alpha
. Рассмотрите два случая.
Решение. Пусть R=12
— радиус окружности. Тогда
AB=2R\sin\angle ACB,~BC=2R\sin\angle BAC.
Отсюда находим, что \sin\angle ACB=\frac{1}{4}
и \sin\angle BAC=\frac{1}{6}
. Поскольку сторона BC
треугольника ABC
— не наибольшая, то угол A
— острый и его косинус положительный. Следовательно,
\cos\angle BAC=\sqrt{1-\sin^{2}\angle A}=\frac{\sqrt{35}}{6},
\cos\angle ACB=\pm\sqrt{1-\sin^{2}\angle C}=\pm\frac{\sqrt{15}}{4}.
Тогда
AC=2R\sin\angle ABC=2R\sin(\angle BAC+\angle ACB)=
=2R(\sin\angle A\cdot\cos\angle C+\cos\angle A\cdot\sin\angle C)=
=2\cdot12\left(\pm\frac{1}{6}\cdot\frac{\sqrt{15}}{4}+\frac{1}{4}\cdot\frac{\sqrt{35}}{6}\right)=\sqrt{35}\pm\sqrt{15}.
Источник: Вступительный экзамен в МАИ. — 1977
Источник: Говоров В. М. и др. Сборник конкурсных задач по математике. — М.: Наука, 1986. — № 39, с. 187
