716. На сторонах AB
и AC
угла BAC
, равного 120^{\circ}
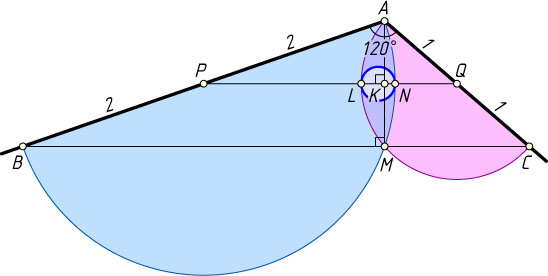
, как на диаметрах построены полуокружности. В общую часть образовавшихся полукругов вписана окружность максимального радиуса. Найдите радиус этой окружности, если AB=4
, AC=2
.
Ответ. \frac{3-\sqrt{7}}{2}
.
Указание. Докажите, что диаметр искомой окружности — отрезок, высекаемый на линии центров данными полуокружностями.
Решение. Пусть r=1
и R=2
— радиусы данных полуокружностей, P
и Q
— их центры, AM
— их общая хорда; K
— точка пересечения отрезков PQ
и AM
, N
и L
— точки пересечения полуокружностей с отрезком PQ
. Найдём NL
.
По теореме косинусов
PQ^{2}=PA^{2}+QA^{2}-2PA\cdot QA\cos120^{\circ}=1+4+2=7,~PQ=\sqrt{7}.
Докажем, что LN
— диаметр искомой окружности. Пусть O
— центр произвольной окружности, вписанной в общую часть данных полукругов, x
— её радиус, F
и T
— точки касания с меньшей и большей полуокружностями. Тогда
PO+OQ\geqslant PQ,~\mbox{или}~r-x+R-x\geqslant r+R-LN
откуда 2x\leqslant LN
.
Следовательно, искомый радиус равен
\frac{1}{2}KL=\frac{1}{2}(r+R-PQ)=\frac{3-\sqrt{7}}{2}.
Источник: Вступительный экзамен в МЭСИ. — 1977
Источник: Говоров В. М. и др. Сборник конкурсных задач по математике. — М.: Наука, 1986. — № 40, с. 187
