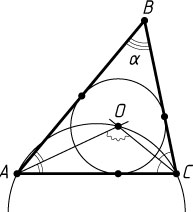
717. В треугольнике ABC
известно, что AC=b
, \angle ABC=\alpha
. Найдите радиус окружности, проходящей через центр вписанного в треугольник ABC
круга и вершины A
и C
.
Ответ. \frac{b}{2\cos\frac{\alpha}{2}}
.
Указание. Докажите, что сторона AC
видна из центра вписанного в треугольник ABC
круга под углом 90^{\circ}+\frac{\alpha}{2}
.
Решение. Пусть O
— центр вписанного в треугольник ABC
круга, R
— искомый радиус.
\angle AOC=180^{\circ}-\frac{1}{2}\angle BAC-\frac{1}{2}\angle BCA=180^{\circ}-\frac{1}{2}(\angle BAC+\angle BCA)=
=180^{\circ}-\frac{1}{2}(180^{\circ}-\angle ABC)=90^{\circ}+\frac{\alpha}{2}.
Тогда
R=\frac{AC}{2\sin\angle AOC}=\frac{b}{2\sin\left(90^{\circ}+\frac{\alpha}{2}\right)}=\frac{b}{2\cos\frac{\alpha}{2}}.
Источник: Вступительный экзамен в МИФИ. — 1978
Источник: Говоров В. М. и др. Сборник конкурсных задач по математике. — М.: Наука, 1986. — № 41, с. 187
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.17, с. 87
