718. Две окружности радиусов R
и r
(R\gt r
) касаются внешне в точке C
. К ним проведена общая внешняя касательная AB
, где A
и B
— точки касания. Найдите стороны треугольника ABC
.
Ответ. 2\sqrt{Rr}
, 2r\sqrt{\frac{R}{R+r}}
, 2R\sqrt{\frac{r}{R+r}}
.
Указание. Опустите перпендикуляр из центра меньшей окружности на радиус большей, проведённый в точку касания с общей внешней касательной. Найдите стороны и косинус острого угла получившегося прямоугольного треугольника.
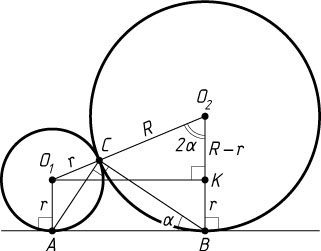
Решение. Пусть O_{1}
и O_{2}
— центры окружностей радиусов r
и R
, A
— точка на первой окружности, B
— на второй, K
— проекция точки O_{1}
на BO_{2}
. Тогда
KO_{2}=BO_{2}-AO_{1}=R-r,~O_{1}O_{2}=r+R,
AB=KO_{1}=\sqrt{O_{1}O_{2}^{2}-KO_{2}^{2}}=\sqrt{(R+r)^{2}-(R-r)^{2}}=2\sqrt{Rr}.
Обозначим \angle ABC=\frac{1}{2}\angle BO_{2}C=\alpha
. Тогда
\cos2\alpha=\frac{KO_{2}}{O_{1}O_{2}}=\frac{R-r}{R+r},~\cos\alpha=\sqrt{\frac{1+\cos2\alpha}{2}}=\sqrt{\frac{1+\frac{R-r}{R+r}}{2}}=\sqrt{\frac{R}{R+r}}.
Поскольку треугольник ACB
— прямоугольный (\angle C=90^{\circ}
), то
BC=AB\cos\alpha=2\sqrt{Rr}\sqrt{\frac{R}{R+r}}=2R\sqrt{\frac{r}{R+r}}.
Аналогично находим AC
.
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) КГУ. — 1977
Источник: Говоров В. М. и др. Сборник конкурсных задач по математике. — М.: Наука, 1986. — № 44, с. 187
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.28, с. 69
