719. Две окружности радиусов R
и r
(R\gt r
) касаются внешним образом. Найдите радиусы окружностей, касающихся обеих данных окружностей и их общей внешней касательной.
Ответ. \frac{Rr}{(\sqrt{R}\pm\sqrt{r})^{2}}
.
Указание. Если данные окружности радиусов r
и R
касаются общей внешней касательной в точках A
и B
соответственно, а искомая — в точке C
, то либо AC+AB=BC
, либо AC+CB=AB
.
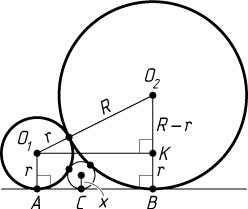
Решение. Пусть O_{1}
и O_{2}
— центры касающихся окружностей радиусов r
и R
, A
и B
— их точки касания с общей внешней касательной.
Опустим перпендикуляр O_{1}K
на O_{2}B
и из прямоугольного треугольника O_{1}KO_{2}
, в котором O_{1}O_{2}=R+r
, O_{2}K=R-r
, находим, что O_{1}K=2\sqrt{Rr}
. Поэтому и AB=2\sqrt{Rr}
.
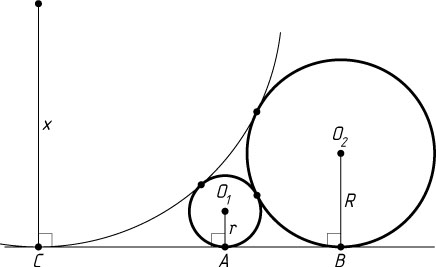
Если x
— радиус искомой окружности, которая касается прямой AB
в точке C
, то аналогично можно доказать, что AC=2\sqrt{rx}
и BC=2\sqrt{Rx}
.
Если точка C
лежит между A
и B
, то AC+BC=AB
. Тогда, решив уравнение 2\sqrt{xr}+2\sqrt{Rx}=2\sqrt{Rr}
, получим, что
x=\frac{Rr}{(\sqrt{R}+\sqrt{r})^{2}}.
В противном случае точка A
лежит между точками B
и C
(так как R\gt r
). Поэтому соответствующее уравнение примет вид
2\sqrt{Rx}-2\sqrt{rx}=2\sqrt{Rr}.
Следовательно, x=\frac{Rr}{(\sqrt{R}-\sqrt{r})^{2}}
.
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 213, с. 22
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 3, с. 179
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.29, с. 69
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 11, с. 7

