720. Две окружности радиусов R
и r
касаются внешним образом в точке A
. На окружности радиуса r
взята точка B
, диаметрально противоположная точке A
, и в этой точке построена касательная l
. Найдите радиус окружности, касающейся двух данных окружностей и прямой l
.
Ответ. \frac{r(R+r)}{R}
или r+R
.
Указание. Примените формулу Герона.
Решение. Первый способ. Если третья окружность касается прямой l
в точке B
, то её радиус равен r+R
.
Пусть теперь третья окружность (с центром Q
и радиусом x
) касается прямой l
в точке C
, отличной от точки B
. Если O_{1}
и O_{2}
— центры окружностей радиусов r
и R
соответственно, то стороны треугольника O_{1}O_{2}Q
равны:
O_{1}O_{2}=r+R,~O_{1}Q=r+x,~O_{2}Q=R+x.
По формуле Герона
S_{\triangle O_{1}O_{2}Q}=\sqrt{(x+R+r)\cdot x\cdot r\cdot R}.
Если QM
— высота этого треугольника, то (см. задачу 365)
QM=BC=2\sqrt{rx},~S_{\triangle O_{1}O_{2}Q}=\frac{1}{2}(r+R)\cdot2\sqrt{rx}.
Решив уравнение
\sqrt{(x+R+r)xrR}=(r+R)\sqrt{rx},
получим, что x=\frac{r(R+r)}{R}
.
Второй способ. Если третья окружность касается прямой l
в точке B
, то её радиус равен r+R
.
Пусть теперь третья окружность с центром Q
и радиусом x
касается прямой l
в точке C
, отличной от точки B
. Если O_{1}
и O_{2}
— центры окружностей радиусов r
и R
соответственно, а M
— проекция точки Q
на прямую O_{1}O_{2}
, то
O_{1}Q=r+x,~O_{2}Q=R+x,~O_{2}M=|R+2r-x|,~O_{1}M=x-r.
По теореме Пифагора O_{2}Q^{2}-O_{2}M^{2}=O_{1}Q-O_{1}M^{2}
, или
(R+x)^{2}-(R+2r-x)^{2}=(r+x)^{2}-(x-r)^{2}.
Из этого уравнения находим, что x=\frac{r(R+r)}{R}
.
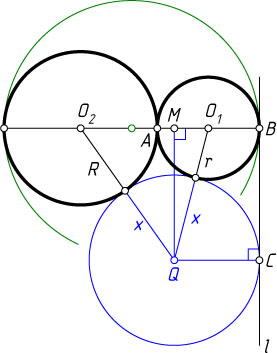
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) КГУ. — 1977
Источник: Говоров В. М. и др. Сборник конкурсных задач по математике. — М.: Наука, 1986. — № 46, с. 187
