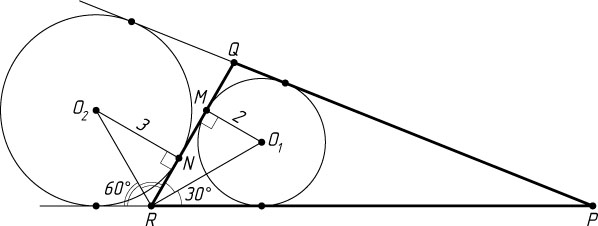
721. В треугольнике PQR
угол QRP
равен 60^{\circ}
. Найдите расстояние между точками касания со стороной QR
окружности радиуса 2, вписанной в треугольник, и окружности радиуса 3, касающейся продолжений сторон PQ
и PR
.
Ответ. \sqrt{3}
.
Указание. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Решение. Пусть O_{1}
и O_{2}
— центры окружностей радиусов 2 и 3 соответственно, M
и N
— их точки касания со стороной RQ
. Тогда
RM=O_{1}M\cos\angle MRO_{1}=2\cos30^{\circ}=2\sqrt{3},
RN=O_{2}N\cos\angle NRO_{2}=3\cos60^{\circ}=\sqrt{3}.
Поэтому
MN=RM-RN=2\sqrt{3}-\sqrt{3}=\sqrt{3}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1980, вариант 3, № 3
Источник: Говоров В. М. и др. Сборник конкурсных задач по математике. — М.: Наука, 1986. — № 48, с. 188
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1983. — с. 14
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.14, с. 87
