723. Из вершины тупого угла A
треугольника ABC
опущена высота AD
. Из точки D
радиусом, равным AD
, описана окружность, пересекающая стороны треугольника AB
и AC
в точках M
и N
соответственно. Найдите сторону AC
, если известно, что AB=c
, AM=m
и AN=n
.
Ответ. \frac{mc}{n}
.
Указание. Докажите, что треугольники AMN
и ACB
подобны.
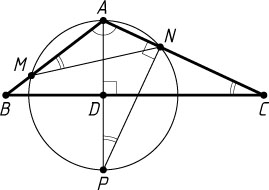
Решение. Продолжим AD
до пересечения с указанной окружностью в точке P
. Тогда \angle AMN=\angle APN
, а так как \angle ANP=90^{\circ}
, то \angle APN=\angle ACB
. Поэтому треугольники AMN
и ACB
подобны. Следовательно,
\frac{AM}{AC}=\frac{AN}{AB}.
Отсюда находим, что
AC=\frac{AB\cdot AM}{AN}=\frac{mc}{n}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1991, № 4, вариант 1
Источник: Журнал «Квант». — 1992, № 2, с. 58
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.22, с. 113
Источник: Всероссийская олимпиада школьников. — 2016-2017, XLIII, окружной этап, 10 класс
