724. В треугольнике ABC
угол C
— тупой, D
— точка пересечения прямой DB
, перпендикулярной к AB
, и прямой DC
, перпендикулярной к AC
. Высота треугольника ADC
, проведённая из вершины C
, пересекает AB
в точке M
. Известно, что AM=a
, MB=b
. Найдите AC
.
Ответ. \sqrt{a(a+b)}
.
Указание. Докажите, что треугольники CAM
и BAC
подобны.
Решение. Поскольку \angle ABD=\angle ACD=90^{\circ}
, то точки A
, C
, B
и D
лежат на окружности с диаметром AD
.
Пусть CN
— высота треугольника ADC
. Продолжим CN
до пересечения с окружностью в точке K
. AD
— диаметр, перпендикулярный хорде CK
, поэтому CN=NK
и AC=AK
. Следовательно,
\angle ACK=\angle AKC=\angle ABC.
Поэтому треугольники CAM
и BAC
подобны по двум углам. Тогда \frac{AC}{AB}=\frac{AM}{AC}
. Отсюда находим, что
AC^{2}=AM\cdot AB=a(a+b).
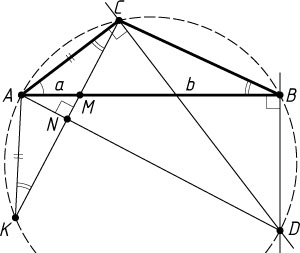
Источник: Вступительный экзамен на физический факультет МГУ. — 1991, № 4, вариант 1
Источник: Журнал «Квант». — 1992, № 2, с. 59
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.23, с. 113
