728. Известно, что в трапецию можно вписать окружность. Докажите, что окружности, построенные на боковых сторонах трапеции как на диаметрах, касаются друг друга.
Указание. Докажите, что расстояние между центрами указанных окружностей равно сумме их радиусов.
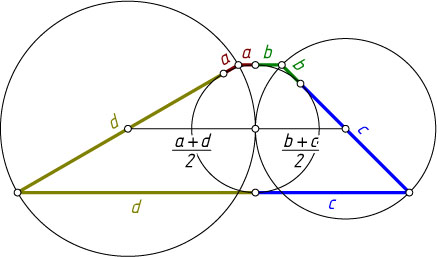
Решение. Отрезок, соединяющий центры указанных окружностей, — средняя линия трапеции. Сумма радиусов окружностей кругов равна полусумме боковых сторон трапеции, или её средней линии (так как трапеция — описанная). Поэтому расстояние между центрами окружностей равно сумме их радиусов. Следовательно, окружности касаются.

Источник: Турнир городов. — 1987-1988, X, весенний тур, старшие классы, тренировочный вариант
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 820, с. 101