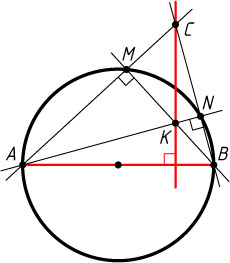
731. Пусть AB
— диаметр окружности, C
— некоторая точка плоскости. Прямые AC
и BC
пересекают окружность в точках M
и N
соответственно. Прямые MB
и NA
пересекаются в точке K
. Найдите угол между прямыми CK
и AB
.
Ответ. 90^{\circ}
.
Указание. Высоты треугольника пересекаются в одной точке.
Решение. \angle AMB=\angle BNA=90^{\circ}
как вписанные углы, опирающиеся на диаметр, поэтому AN
и BM
— высоты треугольника ABC
. Поскольку высоты треугольника пересекаются в одной точке, то прямые CK
и AB
перпендикулярны.
Источник: Журнал «Математика в школе». — № 3, 1989, с. 100, № 100
