732. Окружность высекает на сторонах четырёхугольника равные хорды. Докажите, что в этот четырёхугольник можно вписать окружность.
Указание. Докажите, что центр данной окружности равноудалён от сторон четырёхугольника.
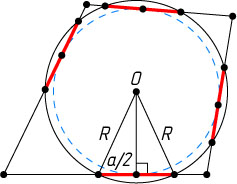
Решение. Пусть R
— радиус данной окружности, a
— длина каждой из указанных хорд, O
— центр окружности. Тогда расстояние от точки O
до каждой стороны четырёхугольника равно \sqrt{R^{2}-\frac{a^{2}}{4}}
. Следовательно, O
— центр окружности, вписанной в данный четырёхугольник.
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 16, с. 196
Источник: Журнал «Математика в школе». — № 3, 1989, с. 102, № 107
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 6.4, с. 152
