733. К окружности проведены касательные, касающиеся её в концах диаметра AB
. Произвольная касательная к окружности пересекает эти касательные в точках K
и M
. Докажите, что произведение AK\cdot BM
постоянно.
Указание. Отрезок KM
виден из центра окружности под прямым углом.
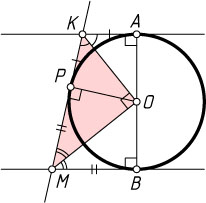
Решение. Пусть O
— центр данной окружности, P
— точка касания с прямой KM
. Тогда
AK=KP,~BM=MP,~\angle OKM+\angle OMK=
=\frac{1}{2}(\angle AKM+\angle BMK)=\frac{180^{\circ}}{2}=90^{\circ}.
Поэтому \angle KOM=90^{\circ}
и OP
— высота прямоугольного треугольника KOM
, опущенная на гипотенузу. Следовательно,
AK\cdot BM=KP\cdot PM=OP^{2}=R^{2},
где R
— радиус данной окружности.
Источник: Журнал «Математика в школе». — № 3, 1989, с. 102, № 110
