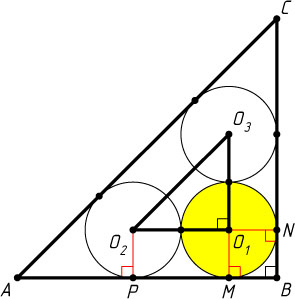
735. В треугольнике ABC
расположены три окружности равных радиусов так, что каждая из окружностей касается двух сторон треугольника. Одна из окружностей (с центром O_{1}
) касается двух других (с центрами O_{2}
и O_{3}
соответственно) и \angle O_{2}O_{1}O_{3}=90^{\circ}
. Установите, что больше: площадь круга, ограниченного окружностью с центром O_{1}
, или пятая часть площади треугольника ABC
?
Ответ. Площадь круга.
Указание. ABC
— равнобедренный прямоугольный треугольник.
Решение. Обозначим через R
радиус окружностей. Пусть окружность с центром O_{1}
касается сторон AB
и BC
в точках M
и N
соответственно, а окружность с центром O_{2}
касается стороны AB
в точке P
. Из условия касания и равенства окружностей следуют соотношения
O_{1}O_{2}=MP=2R,~O_{1}O_{3}=2R,~PO_{2}=MO_{1}=R,
а также параллельность сторон треугольников O_{1}O_{2}O_{3}
и ABC
(BC\parallel O_{1}O_{3}
и AC\parallel O_{2}O_{3}
).
Поскольку \angle O_{2}O_{1}O_{3}=90^{\circ}
, то \angle ABC=90^{\circ}
и треугольник ABC
— равнобедренный и прямоугольный. Тогда
BC=AB=BM+MP+PA=R+2R+R(\sqrt{2}+1)=R(4+\sqrt{2}),
S_{\triangle ABC}=\frac{1}{2}AB\cdot BC=\frac{1}{2}R(4+\sqrt{2})^{2}=\frac{R^{2}(18+8\sqrt{2})}{2}.
Следовательно,
\frac{\frac{1}{5}S_{\triangle ABC}}{\pi R^{2}}=\frac{18+\sqrt{2}}{10\pi}\lt\frac{18+12}{10\pi}=\frac{3}{\pi}\lt1.
Источник: Вступительный экзамен в МФТИ. — 1980, билет 5, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 80-5-3, с. 223
