737. В круге проведены две взаимно перпендикулярные и пересекающиеся хорды AB
и CD
. Известно, что AB=BC=CD
. Установите, что больше: площадь круга или площадь квадрата со стороной AB
.
Ответ. Площадь квадрата.
Указание. Найдите углы треугольника ABC
.
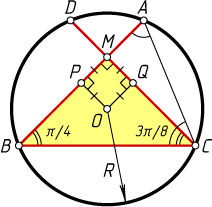
Решение. Пусть M
— точка пересечения хорд AB
и CD
, O
— центр окружности, R
— её радиус, P
и Q
— проекции точки O
на AB
и CD
соответственно.
Тогда MP=QO=PO=MQ
. Следовательно, MB=CM
. Поэтому \angle CBA=\frac{\pi}{4}
, а так как AB=BC
, то треугольник ABC
— равнобедренный. Поэтому
\angle ACB=\frac{\pi-\frac{\pi}{4}}{2}=\frac{3\pi}{8}.
Тогда
AB=2R\sin\angle ACB=2R\sin\frac{3\pi}{8},
и площадь квадрата со стороной AB
равна
AB^{2}=4R^{2}\sin^{2}\frac{3\pi}{8}=2R^{2}\left(1-\cos\frac{3\pi}{4}\right)=
=2R^{2}\left(1+\frac{\sqrt{2}}{2}\right)=R^{2}(2+\sqrt{2}).
Площадь круга равна \pi R^{2}
.
Поскольку 2+\sqrt{2}\gt3{,}4\gt\pi
, то площадь квадрата больше.
