739. Вписанная в треугольник ABC
окружность касается его сторон AC
и BC
в точках M
и N
соответственно и пересекает биссектрису BD
в точках P
и Q
. Найдите отношение площадей треугольников PQM
и PQN
, если \angle A=\frac{\pi}{4}
, \angle B=\frac{\pi}{3}
.
Ответ. \frac{\sqrt{3}-1}{\sqrt{6}}=\frac{2}{\sqrt{3}}\sin\frac{\pi}{12}
.
Указание. Выразите расстояние от точек N
и M
до прямой BD
через радиус окружности.
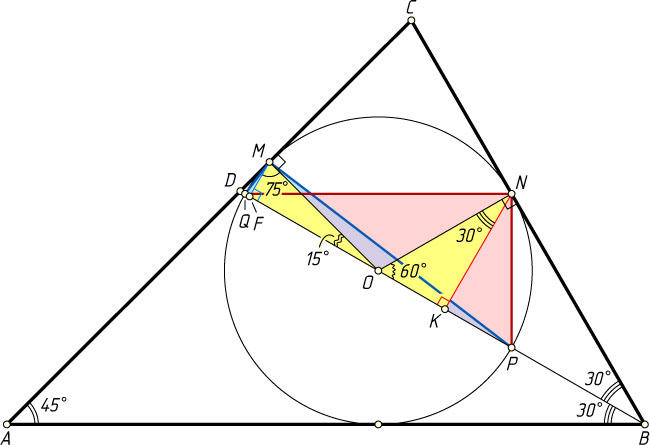
Решение. Пусть R
— радиус вписанной окружности, O
— её центр, F
и K
— проекции точек M
и N
на BD
. Из прямоугольного треугольника NOB
находим, что
\angle NOB=90^{\circ}-\angle NBO=90^{\circ}-30^{\circ}=60^{\circ}.
Из прямоугольных треугольников NKO
и DMO
находим, что
NK=ON\sin\angle NOB=R\sin60^{\circ}=\frac{R\sqrt{3}}{2},
\angle FMO=\angle MDO=\angle CAB+\angle ABD=45^{\circ}+30^{\circ}=75^{\circ}.
Поэтому
MF=MO\cos75^{\circ}=R\sin15^{\circ}.
Следовательно,
\frac{S_{\triangle PQM}}{S_{\triangle PQN}}=\frac{R\sin15^{\circ}}{\frac{R\sqrt{3}}{2}}=\frac{2}{\sqrt{3}}\sin15^{\circ}.
Источник: Вступительный экзамен в МФТИ. — 1979, билет 1, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 79-1-4, с. 211
