741. Окружность, построенная на основании BC
трапеции ABCD
как на диаметре, проходит через середины диагоналей AC
и BD
трапеции и касается основания AD
. Найдите углы трапеции.
Ответ. 30^{\circ}
, 30^{\circ}
, 150^{\circ}
, 150^{\circ}
.
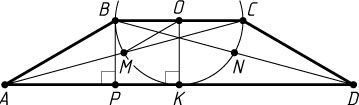
Указание. Если O
— центр окружности, а M
— середина диагонали AC
, то OM
— средняя линия треугольника ABC
.
Решение. Обозначим через R
радиус окружности. Пусть O
— её центр, M
и N
— середины диагоналей AC
и BD
соответственно, K
— точка касания окружности с основанием AD
, P
— проекция вершины B
на основание AD
. Тогда OM=R
— средняя линия треугольника ABC
. Поэтому
AB=2OM=2R,~BP=OK=R.
Из прямоугольного треугольника BAP
находим, что \angle BAP=30^{\circ}
. Аналогично \angle CDA=30^{\circ}
.
Источник: Вступительный экзамен в МФТИ. — 1979, билет 7, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 79-7-3, с. 216
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.27, с. 34
