742. Три прямые проходят через точку O
и образуют попарно углы в 60^{\circ}
. Из произвольной точки M
, отличной от O
, опущены перпендикуляры на эти прямые. Докажите, что основания перпендикуляров являются вершинами правильного треугольника.
Указание. Основания перпендикуляров, точка M
и общая точка прямых лежат на одной окружности.
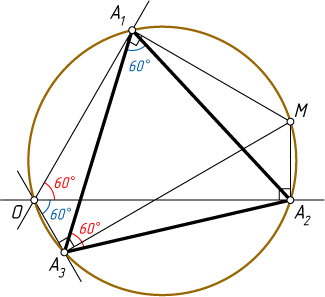
Решение. Предположим, что точка M
расположена, как показано на рисунке. Пусть A_{1}
, A_{2}
, A_{3}
— проекции точки M
на эти прямые.
Поскольку отрезок OM
виден из точек A_{1}
, A_{2}
, A_{3}
под прямым углом, то точки O
, M
, A_{1}
, A_{2}
, A_{3}
лежат на окружности с диаметром OM
. Тогда
\angle A_{2}A_{1}A_{3}=\angle A_{2}OA_{3}=60^{\circ},~\angle A_{1}A_{3}A_{2}=\angle A_{1}OA_{2}=60^{\circ}.
Следовательно, треугольник A_{1}A_{2}A_{3}
— равносторонний.
Аналогично для любого другого положения точки M
.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 15, с. 178
