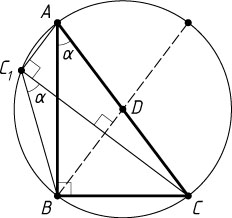
747. В треугольнике ABC
угол B
прямой, величина угла A
равна \alpha
(\alpha\lt\frac{\pi}{4}
), точка D
— середина гипотенузы. Точка C_{1}
симметрична точке C
относительно прямой BD
. Найдите угол AC_{1}B
.
Ответ. \frac{\pi}{2}+\alpha
.
Указание. Докажите, что точка C_{1}
принадлежит окружности, описанной около треугольника ABC
.
Решение. Точка D
— центр окружности, описанной около треугольника ABC
. Поскольку C_{1}D=DC
, то точка C_{1}
принадлежит этой окружности. Поэтому
\angle BC_{1}C=\angle BAC=\alpha,
а \angle AC_{1}C=90^{\circ}
, так как он вписанный и опирается на диаметр AC
. Следовательно,
\angle AC_{1}B=90^{\circ}+\alpha.
Источник: Вступительный экзамен в МФТИ. — 1978, билет № 2, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 78-2-3, с. 202
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.22, с. 104
