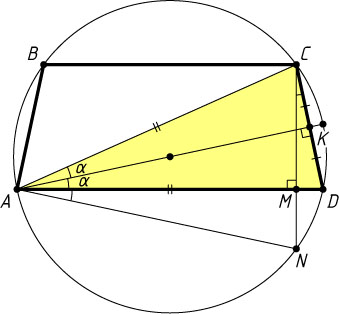
749. В окружность вписана трапеция ABCD
. Диаметр, проведённый через вершину A
, перпендикулярен боковой стороне CD
. Через вершину C
проведён перпендикуляр к основанию AD
, пересекающий отрезок AD
в точке M
, а окружность в точке N
, причём CM:MN=5:2
. Найдите угол при основании трапеции.
Ответ. \arctg\sqrt{5}
.
Указание. Рассмотрите равнобедренный треугольник CAD
.
Решение. Диаметр, перпендикулярный хорде, делит её пополам. Поэтому треугольник CAD
— равнобедренный. Следовательно, его медиана AK
— биссектриса угла CAD
.
Обозначим \angle CAK=\angle KAD=\alpha
. Тогда
\angle NAD=\angle NCD=\angle MCK=\alpha.
Поскольку
\frac{CM}{AM}=\tg\angle CAM=\tg2\alpha,~\frac{MN}{AM}=\tg\angle MAN=\tg\alpha,
то
\frac{CM}{MN}=\frac{\tg2\alpha}{\tg\alpha}=\frac{2}{1-\tg^{2}\alpha}=\frac{5}{2}.
Поэтому 5-5\tg^{2}\alpha=4
. Отсюда находим, что \tg^{2}\alpha=\frac{1}{5}
. Следовательно, \tg\angle CDA=\ctg\alpha=\sqrt{5}
.
Источник: Вступительный экзамен в МФТИ. — 1987, билет 5, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 78-5-4, с. 204
