751. Около окружности описана равнобедренная трапеция ABCD
. Боковая сторона AB
касается окружности в точке M
, а основание AD
— в точке N
. Отрезки MN
и AC
пересекаются в точке P
, причём NP:PM=2
. Найдите отношение AD:BC
.
Ответ. 3.
Указание. Проведите через точку M
прямую, параллельную основаниям трапеции, и рассмотрите получившиеся подобные треугольники.
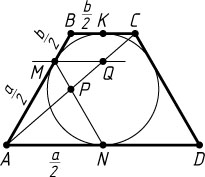
Решение. Пусть K
— точка касания окружности с основанием BC
. Проведём через точку M
прямую, параллельную AD
, до пересечения с диагональю AC
в точке Q
. Обозначим AD=a
, BC=b
. Тогда
AM=AN=\frac{a}{2},~BM=BK=\frac{b}{2}.
Из подобия треугольников MQP
и NAP
находим, что
MQ=\frac{1}{2}AN=\frac{a}{4},
а из подобия треугольников AMQ
и ABC
—
\frac{AM}{AB}=\frac{MQ}{BC},~\mbox{или}~\frac{\frac{a}{2}}{\frac{a}{2}+\frac{b}{2}}=\frac{\frac{a}{4}}{2b}.
Следовательно, a=3b
.
Источник: Вступительный экзамен в МФТИ. — 1978, билет 6, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 78-6-4, с. 205
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 6.18, с. 47
