753. Две окружности радиусов 5 и 3 касаются внутренним образом. Хорда большей окружности касается меньшей окружности и делится точкой касания в отношении 3:1
. Найдите длину этой хорды.
Ответ. 8.
Указание. Из центров окружностей опустите перпендикуляры на данную хорду.
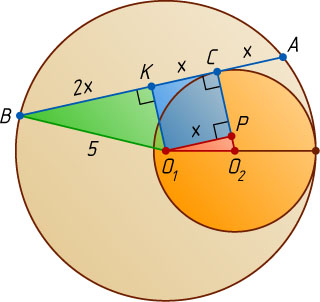
Решение. Пусть O_{1}
и O_{2}
— центры окружностей радиусов 5 и 3 соответственно (рис. 1), AB
— данная хорда, C
— её точка касания с меньшей окружностью (AC:BC=1:3
), P
— проекция точки O_{1}
на радиус O_{2}C
меньшей окружности.
Обозначим AC=x
, тогда BC=3x
. Опустим из центра O_{1}
перпендикуляр KO_{1}
на хорду AB
. Тогда
AK=KB=2x,~CK=AK-AC=x,~O_{1}P=CK=x,
O_{1}O_{2}=2,~O_{2}C=3,~O_{1}K^{2}=O_{1}B^{2}-KB^{2}=25-4x^{2}.
В прямоугольном треугольнике O_{1}PO_{2}
известно, что
O_{1}O^{2}_{2}=O_{2}P^{2}+O_{1}P^{2},~\mbox{или}~4=(3-\sqrt{25-4x^{2}})^{2}+x^{2}.
Из этого уравнения находим, что x=2
. Следовательно, AB=4x=8
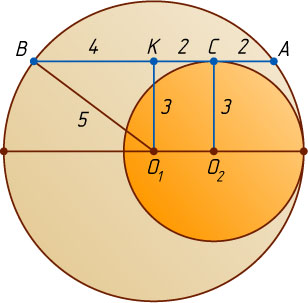
(истинная конфигурация показана на рис. 2).
Источник: Вступительный экзамен в МФТИ. — 1978, билет 9, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 78-9-4, с. 208
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.24, с. 69

