754. Две окружности радиусов 5 и 4 касаются внешним образом. Прямая, касающаяся меньшей окружности в точке A
, пересекает большую в точках B
и C
, причём AB=BC
. Найдите AC
.
Ответ. 12.
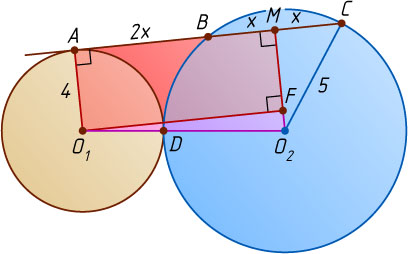
Решение. Пусть окружность радиуса 4 с центром O_{1}
и окружность радиуса 5 с центром O_{2}
касаются внешним образом в точке D
(рис. 1). Тогда O_{1}O_{2}=O_{1}D+O_{2}D=9
.
Опустим перпендикуляр O_{2}M
из центра большей окружности на хорду BC
. Тогда M
— середина BC
. Опустим перпендикуляр O_{1}F
из центра меньшей окружности на прямую O_{2}M
. Тогда AO_{1}FM
— прямоугольник, поэтому MF=O_{1}A=4
и O_{1}F=AM
.
Пусть BM=MC=x
. Тогда AB=BC=2x
и AM=AB+BM=2x+x=3x
. Из прямоугольных треугольников CMO_{2}
и O_{1}FO_{2}
находим, что
O_{2}M=\sqrt{O_{2}C^{2}-MC^{2}}=\sqrt{25-x^{2}},~O_{1}F^{2}+O_{2}F^{2}=O_{1}O_{2},
или
9x^{2}+(\sqrt{25-x^{2}}-4)^{2}=81.
Из этого уравнения находим, что x=3
. Следовательно, AC=4x=12
.
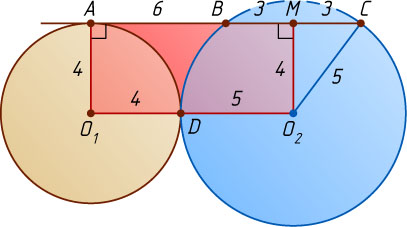
Заметим, что O_{2}M=\sqrt{O_{2}C^{2}-CM^{2}}=\sqrt{25-9}=4=FM
, т. е. точка F
совпадает с O_{2}
(рис. 2).
Источник: Вступительный экзамен в МФТИ. — 1987, билет 11, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 78-11-4, с. 209
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.33, с. 70

