763. Около окружности описана равнобедренная трапеция с основаниями AD
и BC
(AD\gt BC
). Прямая, параллельная диагонали AC
, пересекает стороны AD
и CD
в точках M
и N
соответственно и касается окружности в точке P
. Найдите углы трапеции, если \frac{MP}{PN}=k
(k\lt1
).
Ответ. \arccos\frac{1-k}{\sqrt{k^{2}+1}}
.
Указание. Пусть NL
— высота треугольника MND
. Выразите MN
по теореме косинусов из этого треугольника, учитывая, что ML=ND
.
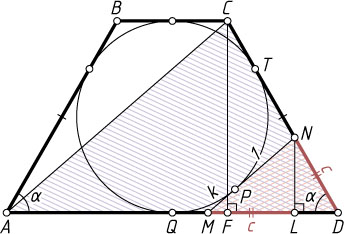
Решение. Пусть MP=k
, PN=1
; Q
и T
— точки касания окружности с основанием AD
и боковой стороной CD
соответственно; F
— проекция вершины C
на основание AD
; L
— проекция точки N
на AD
; \angle CDA=\angle BAD=\alpha
. Тогда
AF=\frac{BC+AD}{2}=\frac{CD+AB}{2}=CD.
Поскольку треугольники NMD
и CAD
подобны, то ML=ND
. Обозначим ND=c
. Тогда
DT=DN+NP=c+1,~DQ=DL+LM+MQ=c\cdot\cos\alpha+c+k,
а так как DT=DQ
, то получим уравнение
c\cdot\cos\alpha+c+k=c+1.
Откуда находим, что c=\frac{1-k}{\cos\alpha}
.
По теореме косинусов в треугольнике NMD
:
MN^{2}=DN^{2}+DM^{2}-2DN\cdot MD\cos\alpha,~\mbox{или}
(1+k)^{2}=c^{2}+c^{2}(1+\cos\alpha)^{2}-2c^{2}(1+\cos\alpha)\cos\alpha=c^{2}(2-\cos^{2}\alpha).
Подставив c=\frac{1-k}{\cos\alpha}
, получим, что
\cos^{2}\alpha=\frac{(1-k)^{2}}{1+k^{2}}.
Примечание. См. также статью Я.Суконника и П.Горнштейна «Геометрические решения геометрических задач», Квант, 1979, N9, с.38-43.
Источник: Вступительный экзамен в МФТИ. — 1974, билет 2, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 74-2-3, с. 168
Источник: Журнал «Квант». — 1979, № 9, с. 42, задача 9
