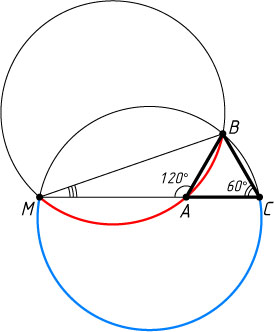
766. На продолжении за точку A
стороны AC
правильного треугольника ABC
взята точка M
, и около треугольников ABM
и MBC
описаны окружности. Точка A
делит дугу MAB
в отношении MA:AB=n
. В каком отношении точка C
делит дугу MCB
?
Ответ. \cup MC:\cup CB=2n+1
.
Указание. Выразите указанные дуги через n
.
Решение. Угол MAB
в первой окружности опирается на дугу MB
. Поскольку \angle MAB=120^{\circ}
, то
\cup MB=240^{\circ},~\cup MAB=120^{\circ}.
Следовательно,
\cup MA=120^{\circ}\cdot\frac{n}{n+1},~\cup AB=\frac{120^{\circ}}{n+1}.
Во второй окружности угол BCM
опирается на дугу MB
. Поскольку \angle BCM=60^{\circ}
, то \cup BM=120^{\circ}
. На дугу BC
второй окружности опирается угол BMC
. Поскольку \angle BMC=\frac{60^{\circ}}{n+1}
, то
\cup BC=\frac{120^{\circ}}{n+1}.
Тогда
\cup MC=360^{\circ}-\cup MB-\cup BC=120^{\circ}\cdot\frac{2n+1}{n+1}.
Следовательно, \cup MC:\cup CB=2n+1
.
Источник: Вступительный экзамен в МФТИ. — 1974, билет 9, № 2
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 74-9-2, с. 173
