769. Две окружности с центрами O_{1}
и O_{2}
пересекаются в точках A
и B
. Первая окружность проходит через центр второй и её хорда BD
пересекает вторую окружность в точке C
и делит дугу ACB
в отношении AC:CB=n
. В каком отношении точка D
делит дугу ADB
?
Ответ. \cup AD:\cup DB=n:(n+2)
.
Указание. Выразите указанные дуги через n
.
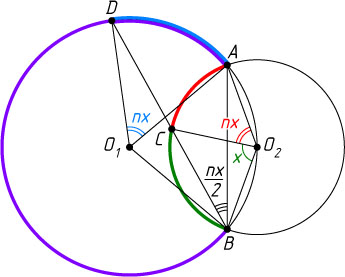
Решение. Обозначим через O_{1}
и O_{2}
центры окружностей. Пусть угловые величины дуг AC
и BC
второй окружности равны nx
и x
. Тогда \angle ABD=\frac{nx}{2}
и угловая величина дуги AD
первой окружности равна nx
.
Из равнобедренного треугольника AO_{2}B
находим, что
\angle O_{2}AB=\frac{1}{2}(180^{\circ}-(n+1)x).
Тогда угловая величина дуги AB
первой окружности в четыре раза больше, т. е.
\cup AB=2(180^{\circ}-(n+1)x),
а угловая величина дополнительной к ней дуги первой окружности равна 2(n+1)x
. Следовательно, искомое отношение равно
\frac{nx}{2(n+1)x-nx}=\frac{n}{n+2}.
Источник: Вступительный экзамен в МФТИ. — 1974, билет 12, № 2
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 74-12-2, с. 176
