770. Стороны AB
и CD
четырёхугольника ABCD
перпендикулярны и являются диаметрами двух равных касающихся окружностей радиуса r
. Найдите площадь четырёхугольника ABCD
, если BC:AD=k
.
Ответ. \frac{3r^{2}(1-k^{2})}{1+k^{2}}
, если k\lt1
,
\frac{3r^{2}(k^{2}-1)}{1+k^{2}}
, если k\gt1
.
Указание. Пусть M
— точка пересечения прямых AB
и CD
. Обозначьте через x
и y
отрезки MB
и MC
и составьте систему уравнений.
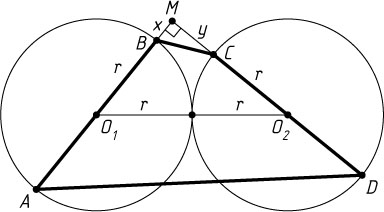
Решение. Обозначим через M
точку пересечения прямых AB
и CD
, O_{1}
и O_{2}
— центры данных окружностей (середины AB
и CD
). Пусть B
и C
принадлежат отрезкам AM
и DM
соответственно. Положим BM=x
, MC=y
. Тогда
BC^{2}=x^{2}+y^{2},~AD^{2}=(x+2r)^{2}+(y+2r)^{2},~O_{1}O^{2}_{2}=(x+r)^{2}+(y+r)^{2}.
Получим систему
\syst{x^{2}+y^{2}=k^{2}((x+2r)^{2}+(y+2r)^{2})\\4r^{2}=(x+r)^{2}+(y+r)^2\\}~\Leftrightarrow~\syst{x^{2}+y^{2}=2k^{2}r(5r+(x+y))\\x^{2}+y^{2}=2r(r-(x+y)).\\}
Из этой системы находим, что x+y=\frac{r(1-5k^{2})}{1+k^{2}}
. Следовательно,
S_{ABCD}=|S_{\triangle AMD}-S_{\triangle MBC}|=\left|\frac{1}{2}(x+2r)(y+2r)-\frac{1}{2}xy\right|=
=|r(x+y)+2r^{2}|=r^{2}\left|\frac{1-5k^{2}}{1+k^{2}}+2\right|=3r^{2}\frac{|1-k^{2}|}{1+k^{2}}.
Источник: Вступительный экзамен в МФТИ. — 1972, билет 6, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 72-6-4, с. 154
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 172, с. 20
