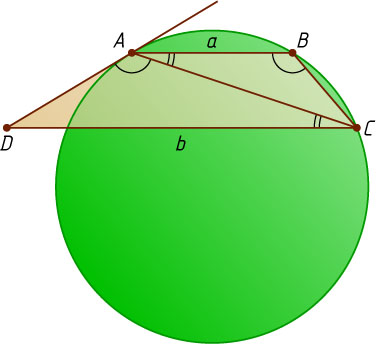
778. В трапеции ABCD
основание AB=a
, основание CD=b
(a\lt b
). Окружность, проходящая через вершины A
, B
и C
, касается стороны AD
. Найдите диагональ AC
.
Ответ. \sqrt{ab}
.
Указание. Треугольники ADC
и BCA
подобны.
Решение. Из теоремы об угле между касательной и хордой следует, что \angle DAC=\angle ABC
.
Поскольку прямые AB
и CD
параллельны, \angle DCA=\angle BAC
. Следовательно, треугольники ADC
и BCA
подобны, поэтому \frac{AB}{AC}=\frac{AC}{CD}
. Отсюда находим, что
AC^{2}=AB\cdot CD=ab.
Источник: Вступительный экзамен в МФТИ. — 1970, билет 11, № 4; 2008, билет 15
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 70-4-11, с. 143
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.20, с. 112
Источник: Шабунин М. И. и др. Методическое пособие по математике для учащихся старших классов и абитуриентов / Под ред. М. И. Шабунина. — 3-е изд. — М.: Физматкнига, 2013. — № 4.215, с. 97
