779. В равнобедренной трапеции с острым углом \alpha
при основании окружность, построенная на боковой стороне как на диаметре, касается другой боковой стороны. В каком отношении она делит большее основание трапеции?
Ответ. \sin2\alpha
.
Указание. Выразите указанные отрезки большего основания через боковую сторону трапеции, т. е. через диаметр окружности.
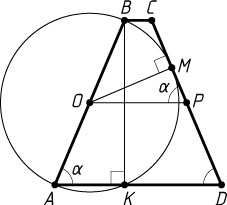
Решение. Пусть O
— центр окружности (середина боковой стороны AB
трапеции ABCD
), OP
— средняя линия трапеции, K
— точка пересечения указанной окружности с большим основанием AD
. Тогда BK
— перпендикуляр к AD
и KD=\frac{1}{2}(AD+BC)=OP
. Если M
— точка касания окружности с боковой стороной CD
, то
OM=\frac{1}{2}AB,~\angle MPO=\angle KAB=\alpha,~KD=OP=\frac{OM}{\sin\alpha}=\frac{AB}{2\sin\alpha},~AK=AB\cos\alpha.
Следовательно,
\frac{AK}{KD}=\frac{AB\cos\alpha}{\frac{AB}{2\sin\alpha}}=2\sin\alpha\cos\alpha=\sin2\alpha.
Источник: Вступительный экзамен в МФТИ. — 1970, № 4, билет 10
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 70-4-10, с. 143
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.24, с. 62
