780. Две равные окружности пересекаются в точке C
. Через точку C
проведены две прямые, пересекающие данные окружности в точках A
, B
и M
, N
соответственно. Прямая AB
параллельна линии центров, а прямая MN
образует угол \alpha
с линией центров. Известно, что AB=a
. Найдите NM
.
Ответ. a\cos\alpha
.
Указание. Опустите перпендикуляры из центров окружностей на прямые AB
и MN
.
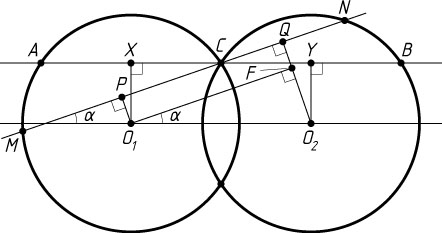
Решение. Пусть O_{1}
и O_{2}
— центры окружностей, точки A
и M
принадлежат первой окружности, B
и N
— второй.
Опустим перпендикуляры O_{1}X
и O_{2}Y
на прямую AB
. Тогда X
и Y
— середины хорд AC
и BC
. Поэтому
O_{1}O_{2}=XY=\frac{1}{2}AC+\frac{1}{2}BC=\frac{1}{2}AB=\frac{a}{2}.
Опустим перпендикуляры O_{1}P
и O_{2}Q
на прямую MN
. Тогда P
и Q
— середины хорд MC
и NC
. Поэтому PQ=\frac{1}{2}MN
.
Пусть F
— проекция точки O_{1}
на O_{2}Q
. Тогда O_{1}F\parallel MN
. Следовательно, \angle FO_{1}O_{2}=\alpha
и O_{1}F=PQ
. Поскольку
O_{1}F=O_{1}O_{2}\cos\alpha=\frac{a}{2}\cdot\cos\alpha,
то
MN=2PQ=a\cos\alpha.
Источник: Вступительный экзамен в МФТИ. — 1974, № 4, билет 9
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 70-4-9, с. 142
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 10.11, с. 77
