782. Две окружности, радиусы которых равны R
и r
, расположены одна вне другой. Отрезки общих внутренних касательных AC
и BD
(A
, B
, C
, D
— точки касания) равны a
. Найдите площадь четырёхугольника ABCD
.
Ответ. \frac{a^{3}(R+r)}{a^{2}+(R+r)^{2}}
.
Указание. Найдите синус угла между диагоналями четырёхугольника ABCD
.
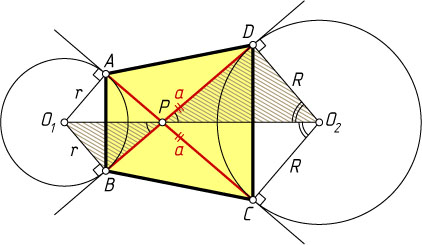
Решение. Пусть O_{1}
и O_{2}
— центры окружностей радиусов r
и R
соответственно, точки A
и B
принадлежат первой окружности, C
и D
— второй, P
— точка пересечения AC
и BD
.
Из подобия треугольников DPO_{2}
и BPO_{1}
следует, что \frac{DP}{PB}=\frac{R}{r}
. Поэтому PD=\frac{Rr}{R+r}
. Следовательно,
\tg\angle DO_{2}P=\frac{DP}{DO_{2}}=\frac{a}{R+r}.
Тогда
\sin\angle DO_{2}C=\sin2\angle DO_{2}P=\frac{\frac{2a}{R+r}}{1+\frac{a^{2}}{(R+r)^{2}}}=\frac{2a(R+r)}{a^{2}+(R+r)^{2}}.
Поэтому
S_{ABCD}=\frac{1}{2}AC\cdot BD\sin\angle DPC=\frac{1}{2}a\cdot a\sin\angle DO_{2}C=
=\frac{1}{2}a^{2}\cdot\frac{2a(R+r)}{a^{2}+(R+r)^{2}}=\frac{a^{3}(R+r)}{a^{2}+(R+r)^{2}}.
Источник: Вступительный экзамен в МФТИ. — 1971, билет 9, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 71-9-3, с. 149
