785. Две окружности касаются друг друга внутренним образом в точке A
; AB
— диаметр большей окружности. Хорда BK
большей окружности касается меньшей окружности в точке C
. Докажите, что AC
— биссектриса треугольника ABK
.
Указание. Докажите, что CO\parallel AK
(O
— центр меньшей окружности).
Решение. Пусть O
— центр меньшей окружности. Поскольку
\angle BCO=\angle BKA=90^{\circ},
то CO\parallel AK
. Поэтому \angle ACO=\angle KAO
, а так как OC=OA
, то треугольник COA
— равнобедренный и \angle ACO=\angle CAO
. Следовательно, \angle KAC=\angle CAO
, т. е. AC
— биссектриса треугольника ABK
.
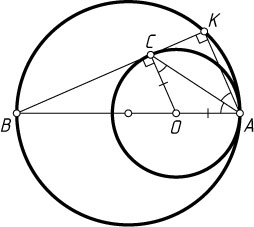
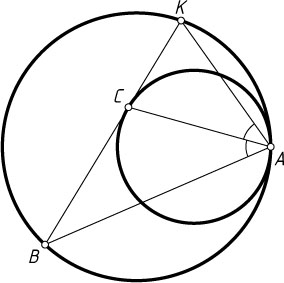
Примечание. Утверждение остаётся верным, если AB
— произвольная хорда большей окружности.
Источник: Задачи по математике и физике, дававшиеся на приёмных испытаниях в 1947—1953 гг. — М.: МФТИ, 1956. — № 4, с. 34

